Modelování v PHP

cze | eng | de

Úvodem

Modelování různých jevů se používá v oblasti technologie a vědy, nicméně jeho výhody je možno využít také ve vzdělávání. Dynamický model a vizualizace jevů modely mohou usnadnit studentům pochopení zkoumaného jevu. Změnou jednoho parametru po malých krocích studenti mohou pozorovat změny celého systému. Dynamické modelování může být použito v případě, že studenti nejsou schopni příklady analyticky spočítat sami. Příspěvek prezentuje možnosti dynamického modelování ve fyzice vyvinuté pomocí PHP na příkladě skládání navzájem kolmých kmitů v rovině, které je doplněné o snadno realizovatelný skutečný 3D model, jehož projekcí do 2D je možno výsledky ověřit.

Skládaní navzájem kolmých kmitů

Grafickým výsledkem skládání navzájem kolmých kmitů v rovině jsou Lissajousovy obrazce (křivky), které se používají k porovnání dvou frekvencí a jejich fází. Jsou-li frekvence navzájem v celočíselném poměru (1:2, 2:3, 5:7, …) jsou obrazce zřetelně viditelné. Navíc, pokud je poměr frekvencí racionální číslo, jsou křivky uzavřené. Pro vytvoření obrazců musíme frekvence „spojit vzájemně kolmo“.

Výsledný pohyb tělesa či bodu při skládání dvou vzájemně kolmých kmitů souměřitelných frekvencí, amplitud a počátečních fází bude periodický pohyb. Ten se bude uskutečňovat po již zmíněných Lissajousových křivkách. Proces výše uvedeného výpočtu by byl manuálně velmi zdlouhavý, a proto můžeme nechat tyto křivky vygenerovat počítač.

Při konstrukci Lissajousových obrazců si můžeme položit následující otázku: "Máme dané frekvence kmitů v jednotlivých osách f_x, f_y a měníme fázi. Je potom každý vytvořený obrazec stejný nebo různý?" Odpověď nám pomůže najít právě dynamické modelování.

Kdo někdy zkusil vytvořit pomocí osciloskopu kterýkoli Lissajousův obrazec, zjistil, že při špatně nastavené časové základně (volt/bod) se začal obrazec pohybovat po obrazovce osciloskopu. Po pečlivějším prozkoumání zjistíme, že to, jak si interpretujeme Lissajousovy obrazce pouze ve 2D není v podstatě úplné. Samotný obrazec si můžeme představit, jako by byl nakreslený na průhledném válcovém tělese po celém jeho obvodu, a my se pouze pohybovali dokola kolem tohoto tělesa a měnil se jenom náš pozorovací úhel. Protože je válec průhledný, vidíme obrazec na bližší stěně i na vzdálenější stěně od nás. Obrazec, který je vytvořený současně „přední“ i „zadní“ projekcí, není tak vždy nový, ale je viděný z jiného místa.

Nutno podotknout, že se tento pohyb místa pozorování kolem válce nemusí být na první pohled zřejmý, protože vzdálenější křivka není menší, chybí nám perspektiva, a to nás přirozeně mate.

Skládaní navzájem kolmých kmitů - ukázka rotace obrazce

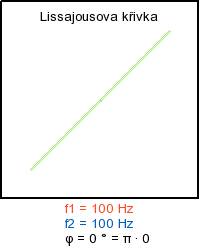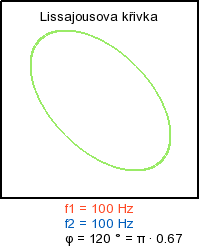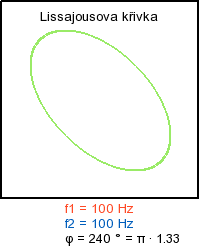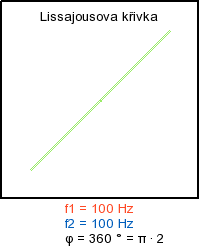
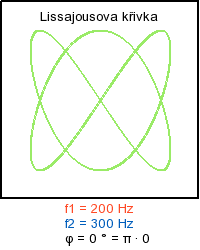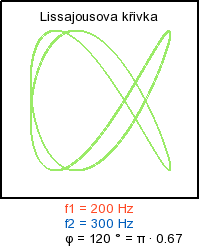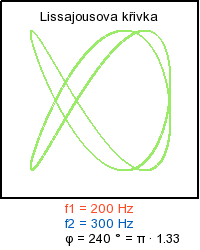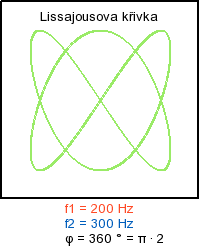
Literatura

BENDL, J. Obrázky a PHP - práce s textem a rozměry Interval.cz [online]. 2003 [cit. 2009-04-16]. Dostupný na Internetu: <http://interval.cz/clanky/obrazky-a-php-prace-s-textem-a-rozmery/>.|
BUREL, D. Grafy, grafy, grafy... a jak na ně v PHP [online]. 2008 [cit. 2009-07-03]. Dostupný na Internetu: <http://programujte.com/?akce=clanek&cl=2007122800-grafy-grafy-grafy-a-jak-na-ne-v-php>. ISSN 1801-1586.
BUREL, D. Úvod do práce s knihovnou GD v PHP [online]. 2008 [cit. 2009-11-23]. Dostupný na Internetu: <http://programujte.com/?akce=clanek&cl=2008010402-uvod-do-prace-s-knihovnou-gd-v-php>. ISSN 1801-1586.
GILMORE, J. Velká kniha PHP 5 a MySQL - kompendium znalostí pro začátečníky i profesionály. Jan Pokorný. Brno : Zoner Press, 2005. 711 s. ISBN 80-86815-20-X.
KONÍČEK, L. Počítačem podporovaná výuka a experiment. Ostrava: Ostravská univerzita v Ostravě, 2003. ISBN 80-7042-965-8.
KOSEK, J. PHP – tvorba internetových aplikací. Praha : Grada Publishing, spol. s r. o., 1998. 490 s. ISBN 80-7169-373-1.
LEPIL, O. Demonstrujeme kmity netradičně. Praha : Prométheus, 1996. 56 s. ISBN: 80-7196-028-4.
LEPIL, O., RICHTEREK, L. Dynamické modelování. Olomouc : Repronis, 2007. 160 s. ISBN 978-80-7329-156-3.
POLÁK, Z., ŠEDIVÝ, P. Vrhy : Studijní text pro řešitele FO č. 46. Hradec Králové. 2002. 32 s.
POTTER, F., PECK, Ch. Dynamic Models in Physics: A Workbook of Computer Simulations Using Electronic Spreadsheets : Mechanics. [s.l.] : N Simonson & Co, 1989. 400 s. ISBN 0962255610.
ROZSYPAL, P. Obrázky v PHP -- Knihovna PHP -- Interval.cz [online]. 2008 [cit. 2009-04-17]. Dostupný na Internetu: <http://php.interval.cz/clanky/obrazky-v-php/>. ISSN 1212-8651.
ŠEDIVÝ, P. Modelování pohybů numerickými metodami : Studijní text pro řešitele FO č. 38. Hradec Králové. 1999. 38 s.
VOLF, I., ŠEDIVÝ, P. Pohyb tělesa v odporujícím prostředí: Studijní text pro řešitele FO č. 17. Hradec Králové. 1995.