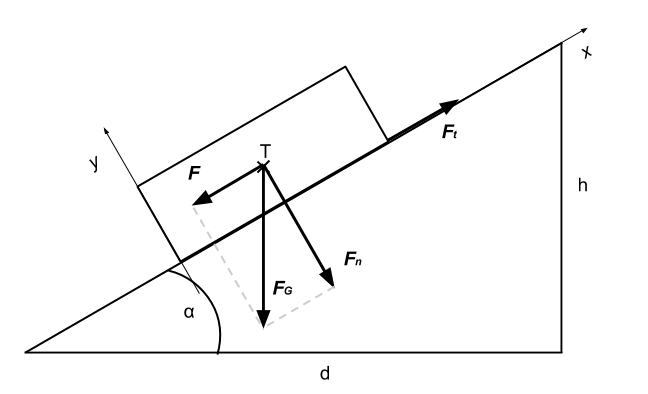
Obr. 1 Zakreslení situace.

Dále již upustíme od vektorového zápisu veličin. A tíhovou sílu F_G rozložíme podle obrázku na složky F (ve směru nakoloněné roviny a F_n (kolmá k nakoloněné rovině).

Třecí síla F_t, která působí na těleso je úměrná normálové síle F_n, kterou těleso působí na nakloněnou rovinu. Podle 3. Newtonova zákona je tato síla stejně velká jako ta, kterou tlačí působí nakloněná rovina na kvádr. Třecí síla pak bude:

Pro určení smykového tření f je pak nutné najít takový sklon nakloněné roviny, při kterém se těleso bude po nakloněné rovině pohybovat rovnoměrným pohybem s udělenou počáteční rychlostí (a = 0). Tedy třecí síla F_t bude kompenzována stejně velkou silou F (ve směru nakloněné roviny), pouze opačného směru než je F_t.

Nebo také z obrázku (Obr. 1)

Kde α úhel naklonění nakloněné roviny, h vodorovný průmět délky nakloněné roviny, d výška zvednutí (naklonění) nakloněné roviny.

Pozn.:

Pokud se těleso po nakloněné rovině pohybuje s nenulovým zrychlením (platí: F > F_t), pak lze zrychlení spočítat:

• Cíl modelu: Doplnění experimentu pro určení hodnoty součinitele smykového tření pomocí nakloněné roviny o grafické znázornění závislosti velikosti třecí síly na úhlu sklonu nakloněné roviny.
• Doporučeno pro: 8. ročník základní školy nebo adekvátní ročníky nižšího gymnázia
• Doporučená délka práce s modelem: 5–10 minut

• Na nakloněnou rovinu položíme kvádr.
• Kvádr uvedeme do pohybu (mírně postrčíme), aby se začal po nakloněné rovině začal pohybovat rovnoměrným pohybem směrem dolů s udělenou počáteční rychlostí. Zrychlení pohybu je nulové (a = 0).
• Měníme sklon nakloněné roviny α, dokud se kvádr nepohybuje směrem dolů rovnoměrným pohybem (stále stejnou rychlostí). Úhel naklonění nakloněné roviny žáci měří úhloměrem nebo spočítají s využitím goniometrických funkcí.
• Změříme délku základny nakloněné roviny na stole d a výšku jejího nejvyššího bodu h.

Pozn.:

• Měření opakujeme s obměnami. Kvádr položíme na nakloněnou rovinu s jiným povrchem (brusný papír, sklo, textil, guma, umělá hmota, kov, ...).
• Provedeme další obměnu měření: navlhčíme nakloněnou rovinu a měření zopakujeme.

function Ft ($f, $m, $g, $alfa) {
	$Ft = $f * $m * $g * cos(deg2rad($alfa));
	return $Ft;
};
function Fx ($f, $m, $g, $alfa) {
	$F = $m * $g * sin(deg2rad($alfa));
	return $F;
};

$alfa = 0;
$dalfa = 0.01;
do{
	$Ft = Ft($f, $m, $g, $alfa);
	$F = Fx($f, $m, $g, $alfa);
	ImageSetPixel($obrazek, $alfa, $Ft, $barva1);
	ImageSetPixel($obrazek, $alfa, $F, $barva2);
	$alfa = $alfa + $dalfa;
} while($alfa <= $max);