Modelování v PHP

cze | eng | de

Volný pád tělesa v odporujícím prostředí

Použité vztahy, doplňující nákresy (kliknutím zobrazit/skrýt)

$\mathbf{F}=\mathbf{F_G} %2B \mathbf{F_O} %2B \mathbf{F_{VZ}}$
$\mathbf{F_G}=m\mathbf{g}$
$\mathbf{F_O}=\frac{1}{2}CS\rho v^2 \mathbf{v^0}$
$\mathbf{F_{VZ}}=V\rho\mathbf{g}$

Kde m je hmotnost tělesa, g gravitační zrychlení, C je součinitel odporu, S plocha kolmá na směr pohybu, ρ je hustota prostředí, v rychlost pohybu tělesa, V objem tělesa.

Vzhledem k tomu, že nás již nyní bude zajímat pouze pohyb v ose y, upustíme od vektorového zápisu veličin. A protože tíhová síla F_G působí v opačném směru než roste osa y, budeme její velikost od celkové síly F odečítat. Naopak síly F_O a F_VZ budeme přičítat.

$F=-F_G %2B F_O %2B F_{VZ}$
$F=-mg %2B \frac{1}{2}C_y S_y\rho v_y^2 %2B V\rho g$

Následně určíme hodnotu zrychlení a_y podělením poseldního vztahu hmotností m. Dále tedy získáváme vztahy pro výpočet zrychlení a_y, rychlosti v_y a polohy y.

$a_y (t)=-g %2B \frac{1}{2m}C_y S_y \rho v_y^2 %2B \frac{1}{m}V\rho g$
$v_y(t + dt) = v_y(t) + a_y(t)dt$
$y(t + dt) = y(t) + v_y(t)dt$

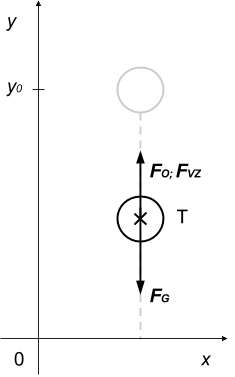
Obr. 1 Zakreslení situace.

Práce s výstupem z počítačového modelu během žákovského experimentu (kliknutím zobrazit/skrýt)

Cíl modelu: Doplnění experimentu demonstrující volný pád v odporujícím prostředí o grafické znázornění závislosti výšky kuličky nad povrchem na čase a srovnání s volným pádem ve vakuu.
Doporučeno pro: 1. ročník vyššího gymnázia
Doporučená délka práce s modelem: 5–10 minut

Postup měření experimentu (kliknutím zobrazit/skrýt)

Pokud máme k dispozici kulové těleso s průměrem d = 0,4 m, můžeme jej pouštět například z balkónu ve 4. poschodí.

Změříme průměr tělesa nebo obvod (poloměr se dopočítá).
Změříme hmotnost tělesa.
Změříme výšku od země, například spuštěním olovnice nebo matky na niti.
Pomocí stopek budeme měřit dobu pádu tělesa.

Pokud máme k dispozici kulové těleso s průměrem d = 0,05 m, můžeme jej pouštět v laboratoři, ale budeme potřebat například soupravu ISES (použijeme například mikrofon, siloměr nebo dvě optické závory).

Změříme průměr tělesa nebo obvod (poloměr se dopočítá).
Změříme hmotnost tělesa.
Změříme výšku od závěsu tělesa k místu dopadu.
Okamžik uvotnění tělesa je snímán siloměrem, dopad zaznamenán mikrofonem.
- Těleso zavěsíme na nit na siloměr.
- Místo dopadu bude snímat mikrofon.
- Počátek pádu tělesa odečteme z odlehčení siloměru.
- Dopad určíme ze sejmutého signálu mikrofonem.
Okamžik uvotnění tělesa je snímán optickými závorami.
- Těleso zavěsíme na nit nad obě optické závory.
- První optická závora je co nejblíže tělesu, ta bude snímat počátek volného pádu.
- Druhá optická závora je co nejblíže místu dopadu, bude snímat konec volného pádu.

Pozn.:

Jako další možnost měření doby volného pádu tělesa, lze použít videoanalýzu pohybu.
Další variantou měření je použití prostředí s vyšší vyskozitou, než má vzduch, například voda, glycerol a další.

Fragment zdrojového kódu modelu (kliknutím zobrazit/skrýt)

function ay ($g, $Cy, $r, $ro, $m, $vy, $eta) {
	$S = pi() * $r * $r;
	$V = 4/3 * pi() * $r * $r * $r;

	$aFoNewton = ($Cy * $S * $ro * $vy * $vy) / (2 * $m);
	$aFvz = ($V * $ro * $g) / $m;

	$ay = 0 - $g + $aFoNewton + $aFvz;
	return $vy;
};
function vy ($v, $ay, $dt) {
	$vy = $v + $ay * $dt;
	return $vy;
};
function yy ($y, $vy, $dt) {
	$yy = $y + $vy * $dt;
	return $yy;
};

$t = 0;
$dt = 0.0001;
$vy = 0;
$yy = $y;
$Sy = pi() * $r * $r;

do{
	$ay = ay($g, $Cy, $r, $ro, $m, $vy, $eta);
	$vy = vy($vy, $ay, $dt);
	$yy = yy($yy, $vy, $dt);
	ImageSetPixel($obrazek, $t, $yy, $barva);
	$t = $t + $dt;
} while($yy >= 0);